

Note that you now have a right triangle formed by (half of) the peak angle of the original triangle, the corner at the circle's center, and the point where the radius line meets the triangle. This radius line, by nature, is perpendicular to the side of the triangle.ĭraw the altitude line of the triangle, thus splitting the triangle into two 30-60-90 triangles. Draw a radius line from the center of the circle to where the circle meets the triangle. :shock:ĭraw the triangle with the pointy corners, and draw a circle inside the peak angle.

So it's not the sides that have a length of 120 millimeters, but the height.
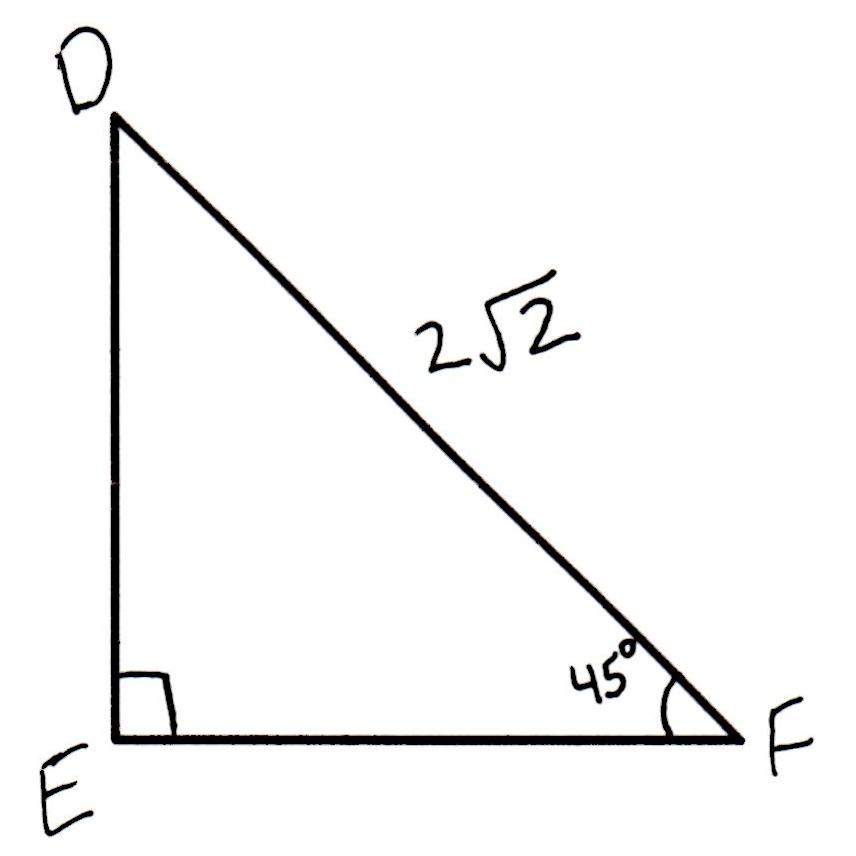
Might you be able to clarify what the 120mm represents?Ĭlick to expand.Ah. If the 120mm is meant to be the given triangle's area (?), then you need only subtract the net change in area as defined above. A = sqrt where a, b, and c are the three sides and s = the semi-perimeter = (a + b + c)/2. If the 120mm is meant to be the given triangle's perimeter, you still need the length of the base, the length of one side or one of the three angles in order to determine the initial area of the isosceles triangle using Heron's area formula The net change in the given isosceles triangle area is therefore The area of the partial circle from B to B is The total area of the 6 triangles so formed at the 3 vertices is The area of the two triangles is Atn = (r)tan(µ/2) Let B be the tangency points of the corner radius on the 2 adjacent sides. Let O be the center of the corner radius r Not having a clear definition as to what "The triangle is 120 mm long" means, consider the geometry of each vertex: The corners are like circles and they have a radius of 10 mm
Isosceles triangle angles in each corner how to#
I'm asked to find the area of an isosceles triangle with rounded corners, and I've got no clue how to do so.


 0 kommentar(er)
0 kommentar(er)
